Uppsättningsteori är nu en del av matematiken. Vi vet alla att en uppsättning kallas varje samling element som tydligt kan särskiljas från varandra och som har en (eller flera) egenskaper gemensamt. Uppsättningsteori studerar uppsättningarnas egenskaper och förhållanden; Detta fält befordrades av Bolzano och Cantor, som senare fulländades redan under 1900-talet av andra matematiker, som Zermelo och Fraenkel.
Det är viktigt att varje uppsättning är perfekt definierad, det vill säga det kan fastställas med precision oavsett om ett objekt ges, det tillhör uppsättningen eller inte.
- I matematik detta är i allmänhet enkelt. Om exempelvis uppsättningen med jämna siffror större än 1 och mindre än 15 beaktas är det uppenbart att denna uppsättning endast kommer att bestå av siffrorna 2, 4, 6, 8, 10, 12 och 14.
- På vanligt språk, att prata om en grupp kan vara mycket mer exakt, för om vi till exempel vill bilda en grupp av de bästa sångarna kommer åsikterna att vara olika och det kommer inte att finnas någon absolut enighet om vem som kommer att vara en del av denna grupp och vem inte. Vissa specialuppsättningar är tomma uppsättningar (saknar element) eller enhetsuppsättningar (med endast ett element).
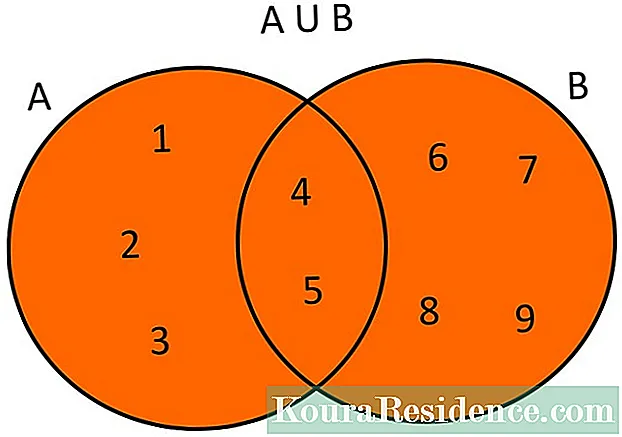
De objekt som ingår i en uppsättning kallas medlemmar eller element, och uppsättningar representeras i skriftliga texter omslutna inom parentes: {}. Inuti staget är föremålen separerade med kommatecken. De kan också representeras av Venn-diagram, som omslutar samlingarna av element som utgör varje uppsättning i en solid och sluten linje, i allmänhet i form av en cirkel. När det finns flera av dessa stängda linjer tilldelas var och en av dem en stor bokstav (A, B, C, etc.) och den globala uppsättningen av dessa representeras av bokstaven U, vilket betyder universell uppsättning.
Med uppsättningarna kan du utföra operationer; de viktigaste är union, korsning, skillnad, komplement och kartesisk produkt. Föreningen av två uppsättningar A och B definieras som uppsättningen A ∪ B och detta innehåller varje element som finns i minst en av dem. Den allmänna ekvationen som representerar den är:
- TILL= {José, Jerónimo}, B= {María, Mabel, Marcela}; AUB= {José, Jerónimo, María, Mabel, Marcela}
- P= {päron, äpple}, C= {citron, apelsin}; F= {körsbär, vinbär};PUCUF = {päron, äpple, citron, apelsin, körsbär, vinbär}
- M={7, 9, 11}, N={4, 6, 8}; MUN={7, 9, 11, 4, 6, 8}
- R= {boll, skridsko, paddla}, G= {paddel, boll, skridsko}; MATTA= {boll, paddel, skridsko}
- C= {daisy}, S= {nejlika}; CUS = {daisy, nejlika}
- C= {daisy}, S= {nejlika}; T= {flaska}, CUSUT = {margarita, nejlika, flaska}
- G= {grön, blå, svart}, H= {svart}; GUH= {grön, blå, svart}
- TILL={ 1, 3, 5, 7, 9 }; B={ 10, 11, 12 }; AUB={ 1, 3, 5, 7, 9, 10, 11, 12 }
- D= {Tisdag, torsdag}, OCH= {Onsdag, fredag}; PÅ GRUND AV = {Tisdag, onsdag, torsdag, fredag}
- B= {mygga, bi, kolibri}; C= {ko, hund, häst}; BUC= {mygga, bi, kolibri, ko, hund, häst}
- TILL={2, 4, 6, 8}, B={1, 2, 3, 4}; AUB={1, 2, 3, 4, 6, 8}
- P= {bord, stol}, F= {bord, stol}; PUQ= {bord, stol}
- TILL= {bröd}, B = {ost}; AUB= {bröd, ost}
- TILL={20, 30, 40}, B= {5, 15}; AUB ={5, 15, 20, 30, 40}
- M= {Januari, februari, mars, april}, N= {November, december}; MUN= {Januari, februari, mars, april, november, december}
- F={12, 22, 32, 42}, G= {a, e, i, o, u}; FUG= {12, 22, 32, 42, a, e, i, o, u}
- TILL= {sommar}, B= {vinter}; AUB= {sommar, vinter}
- S= {sandal, toffel, flip flop}, R= {skjorta}; SÖDER= {sandal, toffel, flip flop, skjorta}
- H= {Måndag, tisdag}, R= {Måndag, tisdag}, D= {Måndag, tisdag}; HURUD= {Måndag, tisdag}
- P= {röd, blå}, F= {grön, gul}, PUQ= {röd, blå, grön, gul}